第 1 頁 (共 2 頁)
98高雄縣第26、46題
發表於 : 2010年 2月 4日, 15:14
由 yaai0307
( )26. 若二元一次聯立方程式 x-3=0
3x+ay=b 無解 ,則下列敘述何者正確?
(A)a=0、b≠9 (B)a=0、b=9 (C)a=-9、b≠0 (D)a=-9、b=0
( )46. 一圓過直線x+y-2=0與圓x +y -2x-y-4=0之交點,又過原點, 下列何者為此圓的方程式?
(A)x +y -x-6=0 (B)x +y -x+ y /2 =0
(C)x +y -4x-3y=0 (D)以上皆非
麻煩老師您了!謝謝。
Re: 98高雄縣第26、46題
發表於 : 2010年 2月 5日, 07:28
由 thepiano
第 26 題
x + 0y = 3
3x + ay = b
由於無解,故 1/3 = 0/a ≠ 3/b
第 46 題
設所求之圓方程式為 x^2 + y^2 - 2x - y - 4 + k(x + y - 2) = 0
由於過原點,以 x = y = 0 代入上式可求出 k = -2
Re: 98高雄縣第26、46題
發表於 : 2010年 2月 5日, 13:30
由 yaai0307
非常謝謝老師您的解答...
不過有一點我還不太明白...
想請教老師
第26題...為什麼 a=0 呢?
Re: 98高雄縣第26、46題
發表於 : 2010年 2月 6日, 09:24
由 thepiano
寫成比的形式,a 在分母,為 0 的確不妥
換另一種方式來說
x = 3 代入 3x + ay = b 得 ay = b - 9
由於該聯立方程無解,故無任何一個 y 值滿足 ay = b - 9
若 a ≠ 0,y = (b - 9) / a,此時該聯立方程是無限多解
若 a = 0,b = 9,此時有無限多組 (3,y) 滿足原本之聯立方程,也是無限多解
故 a = 0,b ≠ 9,聯立方程無解
Re: 98高雄縣第26、46題
發表於 : 2010年 2月 21日, 09:48
由 yaai0307
非常謝謝老師您的講解
謝謝!
Re: 98高雄縣第26、46題
發表於 : 2010年 4月 29日, 09:10
由 wen1019
第46題
設所求之圓方程式為 x^2 + y^2 - 2x - y - 4 + k(x + y - 2) = 0
如何從題目看出要這樣假設呢
能不 請老師告訴我
Re: 98高雄縣第26、46題
發表於 : 2010年 4月 29日, 20:16
由 dream10
一圓過直線x+y-2=0與圓x +y -2x-y-4=0之交點
這一句
Re: 98高雄縣第26、46題
發表於 : 2014年 8月 10日, 17:20
由 acdimns
請問第39題
(有看到用微分的方法解,但我是文組沒學過微分...)
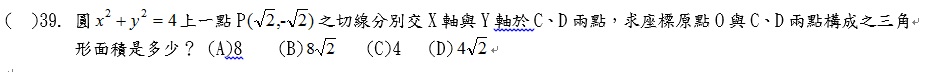
- 1.jpg (23.61 KiB) 已瀏覽 23409 次
ans:C
Re: 98高雄縣第26、46題
發表於 : 2014年 8月 10日, 18:08
由 thepiano
圓心 O(0,0)
直線 OP 之斜率為 -1,由於直線 OP 和直線 CD 垂直,故直線 CD 之斜率為 1
直線 CD 之方程式為 y + √2 = x - √2,即 y = x - 2√2
故 C(2√2,0),D(0,-2√2)
△OCD = 2√2 * 2√2 * (1/2) = 4
Re: 98高雄縣第26、46題
發表於 : 2015年 1月 18日, 15:22
由 doris200121
請問第28.30.36.40.42.47題,謝謝!