第 1 頁 (共 1 頁)
駭客數學 數論 5題
發表於 : 2013年 8月 21日, 23:13
由 acdimns
請教老師5題,很抱歉,因為不會打數學符號,所以都用附檔。
1-3
- IMAG0239_1.jpg (12.19 KiB) 已瀏覽 6818 次
4
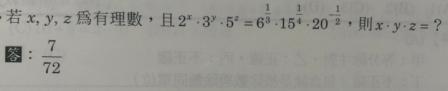
- IMAG0238_1.jpg (4.73 KiB) 已瀏覽 6818 次
5
- IMAG0237_1.jpg (8.21 KiB) 已瀏覽 6818 次
Re: 駭客數學 數論 5題
發表於 : 2013年 8月 22日, 08:13
由 thepiano
第 1 題
2.99^4 - 2.99^3 = 2.99^3 * (2.99 - 1) ＜ 3^3 * 2 = 54
第 2 題
3^16 - 1 = (3^8 + 1)(3^4 + 1)(3^2 + 1)(3^2 - 1) = 6252 * 82 * 10 * 8
第 3 題
2080^2 - 2016^2 = (2080 + 2016)(2080 - 2016) = 4096 * 64 = 2^12 * 2^6 = 2^18
所求 = (2^18)^(1/3) = 2^6 = 64
第 4 題
6^(1/3) * 15^(1/4) * 20^(1/2)
= [2^(1/3) * 3^(1/3)] * [3^(1/4) * 5^(1/4)] * [(2^2)^(-1/2) * 5^(-1/2)]
= 2^(-2/3) * 3^(7/12) * 5^(-1/4)
所求 = 7/72
第 5 題
a 是 16 位數
1 ＜ b ＜ 10，n = 15
Re: 駭客數學 數論 5題
發表於 : 2013年 8月 22日, 16:28
由 acdimns
謝謝老師!
請問,
第一題:
＜54,怎麼不選53呢?是如何判斷?
第四題:
是我沒拍清楚,題目20的次方是（負）-(1/2)
請教最後一個步驟,次方是分數,如3^(7/12)該如何計算?
次方是負數又是分數該如何計算?
Re: 駭客數學 數論 5題
發表於 : 2013年 8月 22日, 16:45
由 thepiano
第 1 題
比 54 小一點，所以整數部份是 53
第 4 題
小弟有老花囉，已更正
3^(1/3) * 3^(1/4) = 3^(1/3 + 1/4) = 3^(7/12)
若次方為負，相乘時也是用加的
Re: 駭客數學 數論 5題
發表於 : 2013年 8月 22日, 18:50
由 acdimns
瞭解了,非常感謝!