第 1 頁 (共 1 頁)
駭客數學 p12-18
發表於 : 2013年 12月 4日, 20:43
由 acdimns
1.
- 03.JPG (32.8 KiB) 已瀏覽 10148 次
2.
- 04.JPG (36.25 KiB) 已瀏覽 10148 次
3.如圖，ACEG 為矩形，GC為對角線，FB∗EC且HD∗ AC，若AB=5cm，BC=2cm，則陰影部分面積佔全部面積 的幾分之幾？
- 02.jpg (7.35 KiB) 已瀏覽 10148 次
ANS:20/49
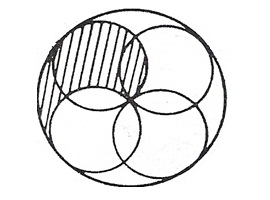
4.下圖中，大圓的半徑是小圓的2倍，試求陰影部分的周長是大圓周長的幾分之幾？
- 01.jpg (16.79 KiB) 已瀏覽 10148 次
ANS:3/4
Re: 駭客數學 p12-18
發表於 : 2013年 12月 4日, 21:26
由 thepiano
第 1 題
令 ∠ABD = x 度，則 ∠ADB = (150 - x) 度
∠CAD = 180 - 30 - 2x = (150 - 2x) 度
∠ADE = [180 - (150 - 2x)]/2 = (x + 15) 度
∠BDE = ∠ADB + ∠ADE = 165 度
∠CDE = 15 度
第 2 題
∠OCD = 90 度
∠BOC = ∠ODC + ∠OCD = 125 度
∠BOC = 90 度 + (1/2)∠A
∠A = 70 度
第 3 題
令 AH = x，GH = y，且 CG 和 BF 交於 P
CB/CA = BP/AG
2/7 = x/(x + y)
y = (5/2)x
所求 = (5x + 2y)/[7(x + y)] = 20/49
第 4 題
見圖
陰影部份周長
= 優弧 AD + 劣弧 CD + 劣弧 BC + 劣弧 AB
= (優弧 AD + 劣弧 CD + 劣弧 AC) + 劣弧 AB
= 小圓周長 + (1/4)大圓周長
剩下的就簡單了......
Re: 駭客數學 p12-18
發表於 : 2013年 12月 5日, 22:51
由 acdimns
都瞭解了,謝謝!
Re: 駭客數學 p12-18
發表於 : 2014年 2月 25日, 00:14
由 shinshin
請問一下老師
上述第二題
如何確定∠OCD = 90 度?
謝謝老師！
Re: 駭客數學 p12-18
發表於 : 2014年 2月 25日, 10:03
由 thepiano
shinshin 寫:如何確定∠OCD = 90 度?
在直線 BC 上取一點 E，使 C 位於 B 和 E 之間
O 是內心，∠ACO = (1/2)∠ACB
D 是旁心，∠ACD = (1/2)∠ACE
∠OCD = ∠ACO + ∠ACD = (1/2)(∠ACB + ∠ACE) = (1/2) * 180度 = 90度
Re: 駭客數學 p12-18
發表於 : 2014年 2月 25日, 12:56
由 shinshin
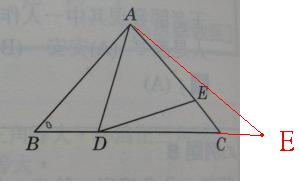
根據老師"在直線 BC 上取一點 E，使 C 位於 B 和 E 之間"
如圖:
- 1.JPG (6.21 KiB) 已瀏覽 10090 次
∠ACD = (1/2)∠ACE?
請問老師,圖是這樣嗎?
怎麼覺得好像有點怪怪的?
Re: 駭客數學 p12-18
發表於 : 2014年 2月 25日, 13:12
由 thepiano
shinshin 寫:怎麼覺得好像有點怪怪的?
是有點怪沒錯，怪在您把第一題的圖看成第二題
Re: 駭客數學 p12-18
發表於 : 2014年 2月 25日, 16:12
由 shinshin
哈哈~謝謝老師耶!
今天思考了好久呢!
