第 1 頁 (共 1 頁)
駭客數學題庫光碟Ch6 P2,5
發表於 : 2014年 3月 1日, 23:37
由 hwm0219

- 圖片1.png (69.29 KiB) 已瀏覽 7521 次
EX11 ANS:A
EX12 ANS:B
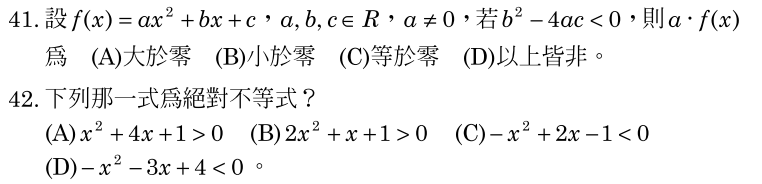
- 圖片2.png (38.54 KiB) 已瀏覽 7521 次
EX41 ANS:A
EX42 ANS:B
Re: 駭客數學題庫光碟Ch6 P2,5
發表於 : 2014年 3月 2日, 11:16
由 thepiano
第 1 題
設甲產品做 x 噸,乙產品做 y 噸
x ≧ 0
y ≧ 0
2x + 6y ≦ 200
4x + 2y ≦ 100
求 6x + 10y 的最大值
畫出以下圖形
x ≧ 0
y ≧ 0
x + 3y ≦ 100
2x + y ≦ 50
可得一四邊形,其頂點為 (0,0),(25,0),(0,100/3),(10,30)
把以上四點的 x 和 y 的值代入 6x + 10y,看哪一個最大就是答案了
第 2 題
見圖
|x - 1| + |y - 1| = 1 的圖形是以 (1,0)、(2,1)、(1,2)、(0,1) 為四頂點的正方形
令 x^2 + y^2 = r^2,它是圓心 (0,0),半徑 r 的圓
此圓在 r = √[(1/2)^2 + (1/2)^2] = √(1/2) 時,跟上述的正方形第一次相切
此圓在 r = √(1^2 + 2^2) = √5 時,跟上述的正方形最後一次相交
故 M = 5,m = 1/2
第 3 題
(1) a > 0
又 b^2 - 4ac < 0
表示 f(x) = ax^2 + bx + c 跟 x 軸無交點且開口朝上
f(x) > 0
a * f(x) > 0
(2) a < 0
又 b^2 - 4ac < 0
表示 f(x) = ax^2 + bx + c 跟 x 軸無交點且開口朝下
f(x) < 0
a * f(x) > 0
第 4 題
不管 x 是任何實數,該不等式都會成立,則稱該不等式為 "絕對不等式"
(B) 選項的判別式 < 0,y = 2x^2 + x + 1 跟 x 軸無交點且開口朝上,故 2x^2 + x + 1 恆 > 0