美夢成真教甄討論區

謝謝解惑

1 + 2 = 3 位於第 1 行第 2 列
1 + 2 + 3 + 4 = 10 位於第 1 行第 4 列
:
1 + 2 + 3 + ... + 20 = 21 * 20 * (1/2) = 210
210 位於第 1 行第 20 列

往右上方倒著數
209 位於第 2 行第 19 列
208 位於第 3 行第 18 列
207 位於第 4 行第 17 列
206 位於第 5 行第 16 列
205 位於第 6 行第 15 列
204 位於第 7 行第 14 列
203 位於第 8 行第 13 列
202 位於第 9 行第 12 列
201 位於第 10 行第 11 列
200 位於第 11 行第 10 列

請教此題，謝謝

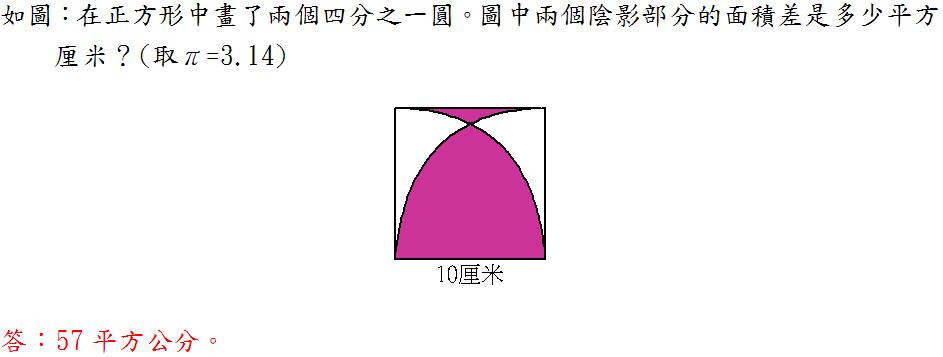
線段 BE 和弧 BE 所圍成的面積 = 扇形 BEC - 正△BEC = (50/3)π - 25√3

線段 AB 和弧 BE 及弧 AE 所圍成的面積 = 扇形 ABE - [(50/3)π - 25√3] = 25√3 - (25/3)π

線段 AD 和弧 AE 及弧 DE 所圍成的面積 = ABCD - 扇形 BCD - [25√3 - (25/3)π] = 100 - 25√3 - (50/3)π

線段 BC 和弧 BE 及弧 CE 所圍成的面積 = 扇形 BEC + [(50/3)π - 25√3] = (100/3)π - 25√3

所求 = (100/3)π - 25√3 - [100 - 25√3 - (50/3)π] = 50π - 100 = 57

另解
設大塊的面積為 A，小塊的面積為 B

扇形 ABC + 扇形 BCD - A + B = ABCD
25π + 25π - A + B = 100
A - B = 50π - 100 = 57