第 1 頁 (共 2 頁)
99台北縣略解
發表於 : 2011年 8月 21日, 02:00
由 someone
除了中間有三題連抄96苗栗縣之外,其他都向台北看齊,沒甚麼考大學數學。這次沒加題目,請自行下載。
因為加了題目,我傳了半個小時還傳不上來。放棄。
Re: 99台北縣略解
發表於 : 2011年 8月 21日, 23:29
由 ksjeng
老師,您好
我試著把圖檔傳上來
有需要的話
就由我來協助
上傳檔案

- 99_箏_蝮__銝剜_撣怎__豢摮貉岫憿_蝑_-page-002.jpg (154.72 KiB) 已瀏覽 29771 次

- 99_箏_蝮__銝剜_撣怎__豢摮貉岫憿_蝑_-page-003.jpg (147.37 KiB) 已瀏覽 29771 次
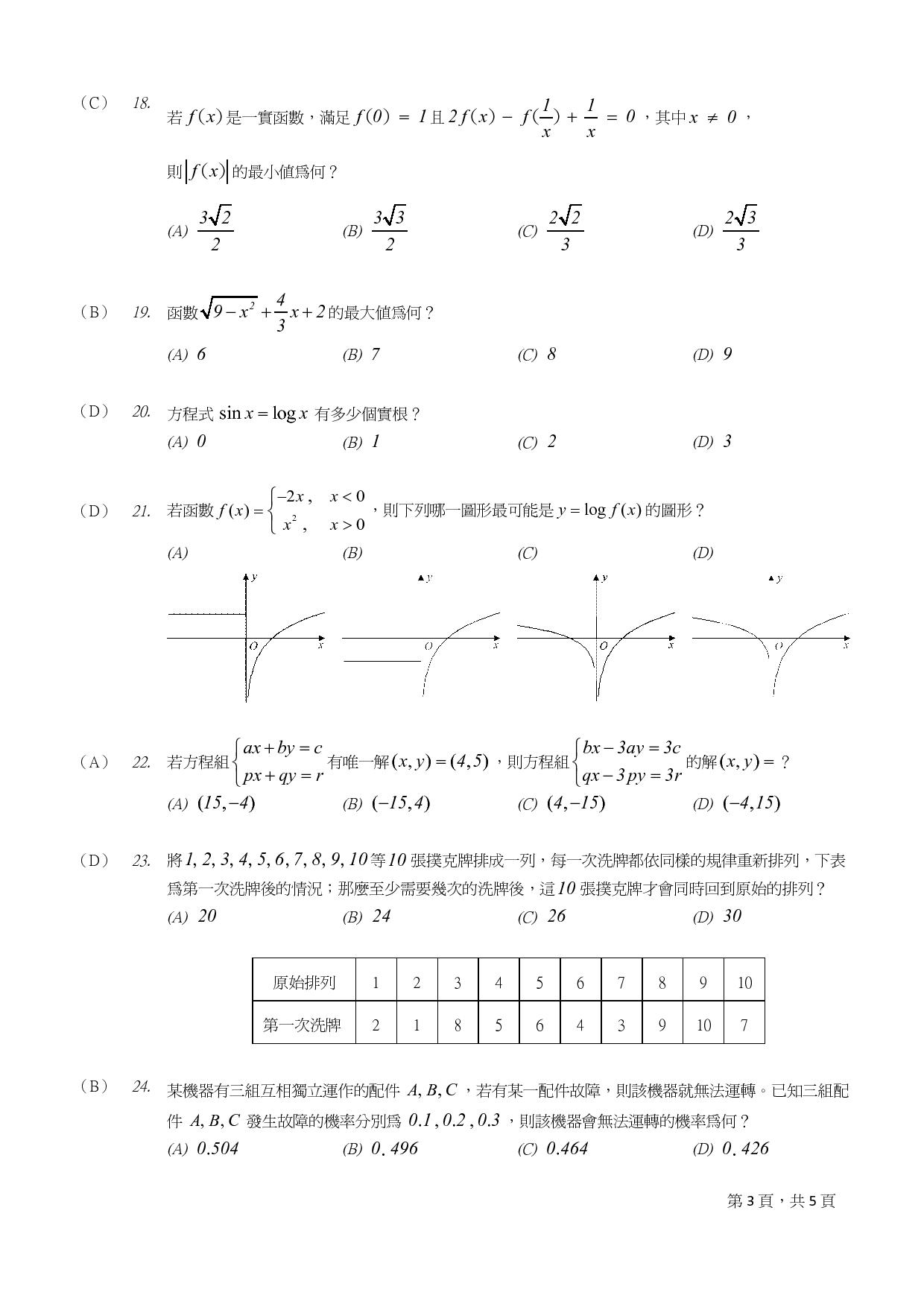
- 99_箏_蝮__銝剜_撣怎__豢摮貉岫憿_蝑_-page-004.jpg (155.56 KiB) 已瀏覽 29771 次

- 99_箏_蝮__銝剜_撣怎__豢摮貉岫憿_蝑_-page-005.jpg (192.59 KiB) 已瀏覽 29771 次

- 99_箏_蝮__銝剜_撣怎__豢摮貉岫憿_蝑_-page-006.jpg (149.84 KiB) 已瀏覽 29771 次
Re: 99台北縣略解
發表於 : 2011年 8月 21日, 23:45
由 someone
我是懶而已,連snagit都懶得再裝在新買的NB上。 XD
Re: 99台北縣略解
發表於 : 2011年 8月 22日, 13:49
由 aikia
感謝分享 ^^
Re: 99台北縣略解
發表於 : 2012年 5月 30日, 23:37
由 Superconan
#7
想請問解題想法,怎麼出現 [10000/(5+1)]+1 這個式子?
#9
令 n = 2^a * 3^b 後面那個聯立方程式怎麼來?
#16
則 (a‧b)/|b|^2 要有最大值
應改成「(a‧b)/|b| 要有最大值」
#29
想問下面解法ok嗎?謝謝!
Z = (x-μ)/σ = (x-65)/4
P(Z>0.675)=0.25
=> P((x-65)/4>0.675)=0.25
=> P(x>65+4*0.675)=0.25
=> P(x>67.7)=0.25
Re: 99台北縣略解
發表於 : 2012年 5月 31日, 13:38
由 thepiano
第 7 題
中括號是高斯記號
若得到 [10000/6] = 1666 票,還不能確定進決賽
因為可能有 6 家都得到 1666 票
再加 1 票的話,就能確定進決賽了
第 9 題
n = 2^a * 3^b 有 (a + 1)(b + 1) 個因數
若 (a + 1)(b + 1) 是偶數
則 n 的所有正因數由小排到大,取頭和尾相乘都會等於 2^a * 3^b
全部正因數之乘積 = (2^a * 3^b)^[(a + 1)(b + 1)/2]
Re: 99台北縣略解
發表於 : 2012年 6月 2日, 16:28
由 Superconan
第 7 題
為什麼是除以6呢?而不是除以5或其它?
第 9 題
那(a + 1)(b + 1)是奇數的情況不需要討論嗎?
謝謝!
Re: 99台北縣略解
發表於 : 2012年 6月 2日, 21:30
由 thepiano
第 7 題
除以 5 沒意義,每家都拿 10000/5 = 2000 票,這篤定進決賽
題目要的是"最少"要拿幾票!
可用 "鴿籠原理" 或 "抽屜原理" 去搜尋相關文章閱讀
第 9 題
若這題是計算題,當然要考慮 n 是完全平方數的情形
但實際上以此題給的 P(n),n 不可能是完全平方數
您可想想看一個完全平方數的所有正因數乘積為何
Re: 99台北縣略解
發表於 : 2012年 6月 3日, 01:49
由 Superconan
第七題
不好意思我有讀過鴿籠原理的相關文章
我知道他在講什麼,但我無法跟這題聯想在一起
也因此不知道要怎麼用鴿籠原理的想法來解這題

第九題
P(1) = 1
P(4) = 1*2*4 = 2^3
P(9) = 1*3*9 = 3^3
P(16) = 1*2*4*8*16 = 2^10
P(25) = 1*5*25 = 5^3
P(36) = 1*2*4*6*9*18*36 = (2^7)*(3^7)
P(144) = 1*2*3*4*6*8*9*12*16*18*24*36*48*72*144 = (2^30)*(3^15)
找了這麼多例子,我還是看不出為何此題的n不可能為完全平方數

Re: 99台北縣略解
發表於 : 2012年 6月 3日, 10:26
由 someone
Superconan 寫:第七題
不好意思我有讀過鴿籠原理的相關文章
我知道他在講什麼,但我無法跟這題聯想在一起
也因此不知道要怎麼用鴿籠原理的想法來解這題

第九題
P(1) = 1
P(4) = 1*2*4 = 2^3
P(9) = 1*3*9 = 3^3
P(16) = 1*2*4*8*16 = 2^10
P(25) = 1*5*25 = 5^3
P(36) = 1*2*4*6*9*18*36 = (2^7)*(3^7)
P(144) = 1*2*3*4*6*8*9*12*16*18*24*36*48*72*144 = (2^30)*(3^15)
找了這麼多例子,我還是看不出為何此題的n不可能為完全平方數

鴿籠原理不妨想成最不幸的狀況,也就是最平均的狀況。
六個人要搶一萬票,最平均的狀況就是每個人都有1666票。還剩四票。
換句話說,只要再多拿一票就穩勝不敗。
平方數的正因數個數必為奇數。
