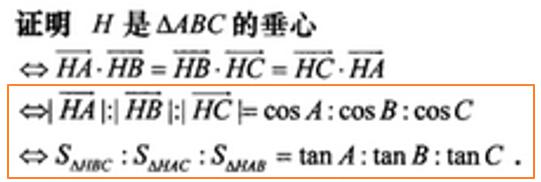
三角函數

[jamesbondmartin]

老師您好, 想請問以下證明過程(圈起來的地方)

[thepiano]

(1)
設三高 AD、BE、CF 交於 H
HC = CE / sin∠EHC = (BC * cosC) / sinA = 2RcosC (R 是外接圓半徑)
同理 HB = 2RcosB，HA = 2RcosA
HA：HB：HC = cosA：cosB：cosC

(2)
△ABD / △ACD = BD / CD
△HBD / △HCD = BD / CD
△HAB / △HAC = (△ABD - △HBD) / (△ACD - △HCD) = BD / CD = (AD/tanB) / (AD/tanC) = tanC / tanB

同理 △HBC / △HAC = tanA / tanB

△HBC： △HAC：△HAB = tanA：tanB：tanC

[jamesbondmartin]

謝謝老師